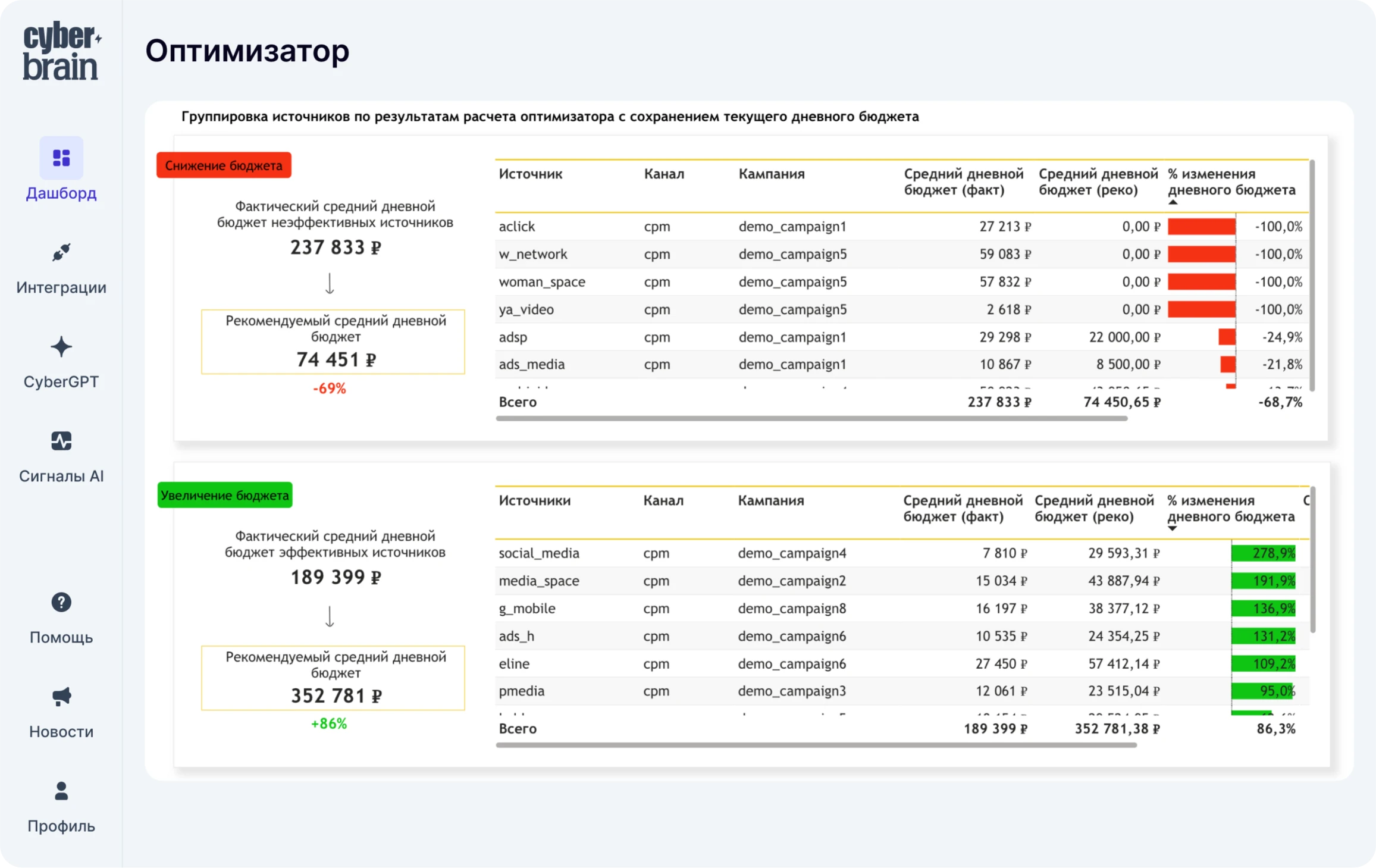
Data driven атрибуция: сравнение моделей Шепли и Маркова

Алгоритмические модели атрибуции помогают честно распределять вклад каналов в конверсии и принимать решения об оптимизации рекламного бюджета. Среди data driven подходов чаще всего сравнивают модель Маркова (Markov Chains) и модель Шепли (Shapley Attribution). Разберёмся, как они работают, в чём их сильные и слабые стороны и почему в ряде задач компании выбирают Shapley.

Data driven модели атрибуции: контекст

Рассматриваем две data driven модели атрибуции, которые присваивают веса точкам взаимодействия на основе теории вероятностей и кооперативных игр: цепи Маркова и значение Шепли соответственно.

• Модель Шепли основана на теории кооперативных игр (Ллойд Шепли, нобелевский лауреат). Варианты Shapley value широко используются в индустрии как основа атрибуции на основе данных.
• Подход Маркова к маркетинговой атрибуции получил популярность благодаря доступности: готовые пакеты, понятная логика «что будет, если убрать канал».

Модель Маркова (Markov Chains): как работает и когда применять

Высокая известность модели связана с доступностью и относительной независимостью от инфраструктуры. Есть открытые пакеты (например, для R), которые позволяют применить метод на предобработанных данных даже без серьёзной ML-инфраструктуры.

Это привлекательно для старта: можно быстро проверить, работает ли атрибуция на основе данных для вашего бизнеса, не будучи одновременно data-scientist, data-инженером и DevOps. Часто хватает ресурсов обычного рабочего окружения.

Идея метода. Марков воспринимает путь как последовательность переходов между каналами и оценивает, как изменится итог, если удалить конкретный шаг (removal effect). Модель учитывает позицию и порядок касаний:

1. проверяем, что будет, если убрать событие/канал из цепочек;
2. пересчитываем вероятность конверсии;
3. вклад канала — разница между исходной и новой вероятностью.

Практические ограничения.
— В сложных многоканальных кампаниях модель порой переоценивает охватные медийные касания, потому что:
a) первый шаг часто получает повышенную ценность (знакомит с продуктом),
b) веса одного и того же канала могут суммироваться по переходам.
— Как вероятностная модель, Марков чувствителен к шуму и требует усреднения/стабилизации.

Когда подходит модель Маркова:

• для старта работы с атрибуцией на основе данных,
• когда экосистема — в основном performance-каналы,
• когда мало или нет медийных источников (низкая доля post-view).

Если компания значимо инвестирует в охватные инструменты, результирующая картина может смещаться в пользу медийки.

Модель Шепли (Shapley Attribution): как работает и когда применять

В этом случае акцент смещается с «порядка касаний» на состав коалиций каналов. Для Шепли важнее не позиция игрока в цепочке, а итог «игры»: что получилось у разных комбинаций каналов.

Суть метода. Вектор (значение) Шепли — принцип справедливого распределения выигрыша между игроками. Мы усредняем маржинальный вклад каждого канала по всем возможным порядкам его подключения к другим каналам. На входе — игроки (каналы), набор игр (цепочек) и результаты; на выходе — суммарный средний вклад каждого канала во всех розыгрышах.

По итогу модель отвечает, насколько конкретный канал повлиял на результат: был ли он вспомогательным или играл ключевую роль. Каждый инструмент оценивается как самостоятельный элемент, и data driven атрибуция определяет, кто действительно «тащит» конверсии в различных комбинациях.

Когда подходит Шепли:

• многоканальные воронки с ощутимой долей медийных и бренд-активностей,
• необходимость честно распределить вклад в условиях сильных взаимодействий между каналами,
• команды, которые опираются на сквозную аналитику и регулярно перераспределяют бюджет по вкладу.

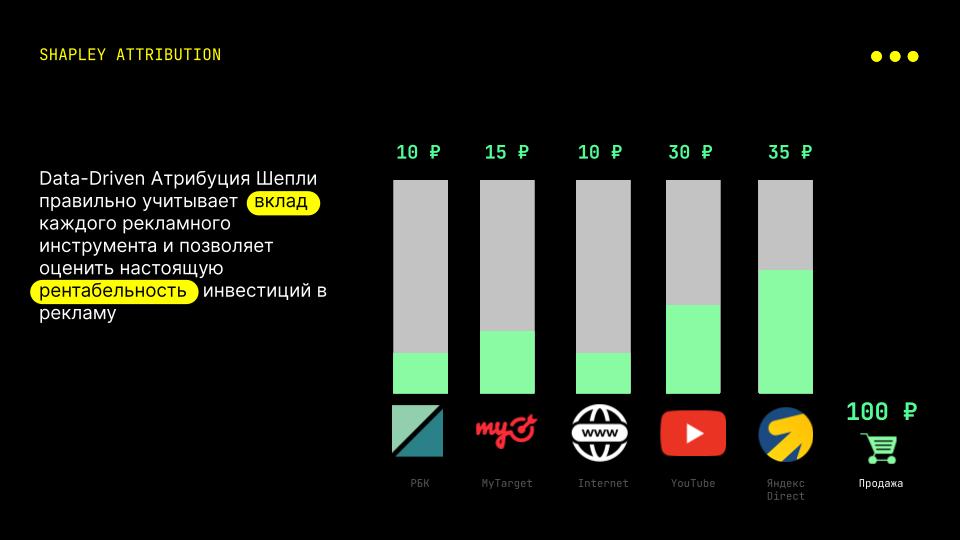
Отличительная особенность Вектора Шепли — аксиома болвана. Болваном в теории кооперативных игр называется бесполезный игрок, не вносящий вклада ни в какую коалицию. Система видит реальные результаты инструмента в динамике и в масштабе тысяч цепочек.

Резюмируя, модель Шепли избавлена от переспама по показам и от проблемы переоценки первого контакта. Она не смотрит на конкретные события: показы, клики, переходы — и их позиции в цепочке, а оценивает итог розыгрыша в целом, то есть справедливо атрибутирует вклад каждого элемента.

Найдя фундаментальное применение в большом количестве разных направлений, она используется, например в Google DCM и в ряде продуктов Adobe. Она доказала свою эффективность в том числе и на маркетинговом рынке и имеет для этого качественное математическое обоснование.

Ключевые отличия (коротко)

• Марков: фокус на последовательности переходов; вклад через «удаление канала».
• Шепли: фокус на комбинациях каналов; вклад как средний маржинальный эффект по всем порядкам.

Зачем это бизнесу

Обе модели — алгоритмические (data driven) инструменты атрибуции, которые помогают честно оценивать эффективность рекламных каналов и принимать решения по оптимизации рекламного бюджета. Выбор зависит от структуры воронки, доли медийки, объёма данных и зрелости инфраструктуры.

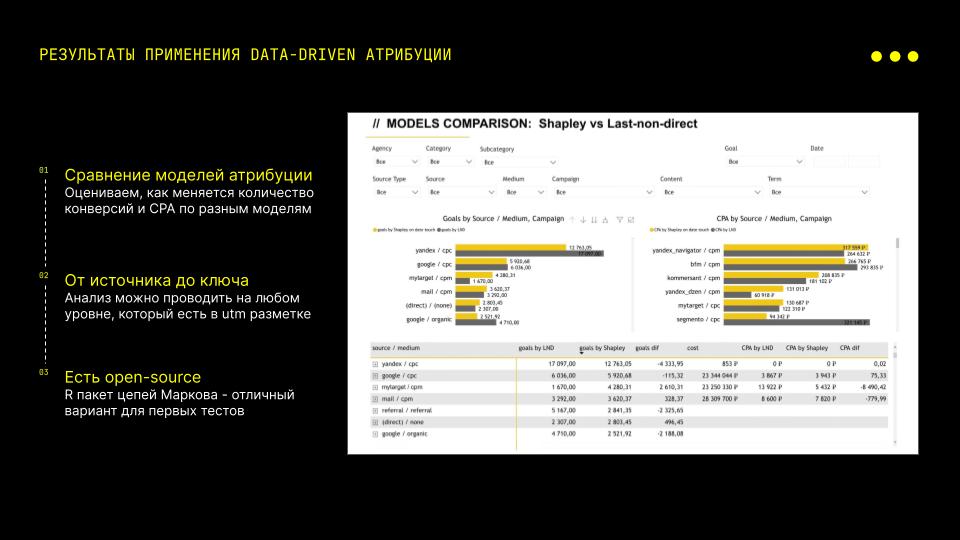
Атрибуция в маркетинге

Согласно Википедии, маркетинговая атрибуция — это идентификация набора действий пользователя («событий» или «точек взаимодействия») по отношению к цели или конверсии, а затем присвоение значения каждой из этих точек взаимодействия.

Цель маркетинговой атрибуции — получить реальное представление о том, какое событие или какая комбинация на желаемое поведение пользователя в достижении цели.

Бизнесы, которые одновременно проводят контекстные кампании с помощью Яндекс Директа, баннерные — в РСЯ или во Вконтакте, а также запускают мобильную, оффлайн и даже телевизионную рекламу, хотят точно знать, что работает хорошо, а что — плохо, или вовсе не работает.

Чтобы бизнес не терял бюджет, который уходит на конвейерную и бесполезную проверку рекламных гипотез, необходима правильная аналитика. Это значительно упрощает оптимизацию, что позволяет видеть реальную производительность каждого канала в цепочке и, в итоге, делать маркетинг рентабельнее. Модели атрибуции на основе данных как раз позволяют маркетологам оценивать реальные вклады событий в конечную цель кампаний.

McKinsey & Co заявляют, что от 15% до 20% маркетинговых бюджетов ежегодно расходуются впустую и могут быть реинвестированы в другие виды деятельности с большей пользой для бизнеса.

Помимо алгоритмических моделей на рынке существуют и прочие виды, поэтому ниже кратко опишем каждый.

Типы моделей

• Модель атрибуции по первому кликуПользователь увидел пост во Вконтакте и попал на ваш сайт через профиль компании. Он посетил сайт еще 3 раза и конвертировался несколько недель спустя. Все заслуги принадлежат первому касанию — органическому Вконтакте.
• Модель атрибуции по последнему кликуПользователь посещает блог на сайте еженедельно в течение 6 месяцев. Сегодня он увидел объявление во Вконтакте со скидкой на ваш продукт и купил его. Все заслуги принадлежат этой рекламе во Вконтакте.
• Модель атрибуции по последнему непрямому кликуПользователь много раз заходил на ваш сайт из разных источников. Он увидел распродажу зимних комплектов через ретаргетинговую рекламу Яндекс и нажал на нее. Возникли проблемы с оплатой, он ушел с сайта и не совершил покупку, вернулся на следующий день, введя ваш сайт прямо в строку поиска и купил его. Кредиты по-прежнему принадлежат этому ретаргетинговому объявлению Яндекс.
• Линейная модель атрибуцииПользователь впервые попал на ваш сайт через блог. Потом он снова пришел из соцсетей. А потом зашел на сайт из рекламы Яндекс и конвертировался. Каждая точка контакта получает равный вес.
• Модель атрибуции на основе позиции (U-образная модель атрибуции)Первая и последняя точки взаимодействия получают по 40% веса каждая, а остальные точки касания делят оставшиеся 20%.
• W-образная модель атрибуции90% кредита поровну распределяется между тремя точками взаимодействия: первое касание, создание лида и конверсия. Оставшиеся 10% распределяются между другими событиями пути.
• Модель атрибуции Time DecayПользователь впервые попал на ваш сайт через блог. Потом он снова пришел из соцсетей. А потом зашел на сайт из рекламы Яндекс и конвертировался. Больше всего кредитов получает Яндекс, затем социальные сети, а затем органические (наиболее далекие от конверсии).
• Модель атрибуции по последнему клику в Google РекламеПользователь был на вашем сайте 2 раза. Затем пришел снова через объявление Google Ads. После этого несколько раз заходил на сайт из многих источников, кроме Google Ads. Хотя изначально конвертировался по прямому заходу на сайт. Вся ценность присваивается рекламе в Google, то есть событию в середине пути.
• Модель атрибуции Lead Conversion TouchПользователь нашел ваш блог через органический поиск, подписался и стал лидом. Вы прогрели его, и он купил ваш продукт. Вся ценность присваивается органике, так как лидом он стал оттуда.
• Полноценная (Z-образная) модель атрибуции:90% кредита поровну распределяется между четырьмя основными каналами: первое касание (22,5%), лидогенерация (22,5%), создание возможностей прихода к конверсии (22,5%), закрытие клиента (22,5%). Оставшиеся 10% распределяются между остальными событиями.
• Пользовательская, алгоритмическая или управляемая данными (data driven) модель атрибуцииСамая точная и продвинутая. Она выполняет углубленный анализ пути клиента, чтобы определить все маркетинговые каналы, играющие роль в привлечении посетителей на веб-сайт и конвертация их в клиентов, а также в присвоении событиям той ценности, которую они заслуживают, исходя из правил конкретной модели.

FAQ

Как работает атрибуция Маркова?
Через removal effect: убираем канал из цепочки и пересчитываем вероятность конверсии.

Чем Шепли отличается от Маркова?
Марков смотрит на реальную последовательность касаний, Шепли — на вклад в разные комбинации каналов.

Можно ли отрицательный вклад?
В Шепли — только ноль, отрицательного вклада быть не может.

Сколько данных нужно?

• Марков: от нескольких сотен конверсий и десятков тысяч сессий.
• Шепли: лучше 1000+ конверсий и полные цепочки, иначе результаты будут случайными.

Как считать в РФ-стеке?
Обе модели можно реализовать на данных Яндекс.Метрики, AppMetrica, VK Ads и CRM. CyberBrain делает это в ClickHouse и встроенном модуле Shapley Attribution.

Выводы

• Марков — удобный старт для performance-компаний и коротких цепочек.
• Шепли — более справедливый и устойчивый метод для многоканальных и медийных стратегий.
• Лучший эффект даёт комбинация: Марков помогает понять структуру пути, а Шепли — честно распределить бюджеты.

Резюме

Чтобы начать работу с моделями атрибуции на основе данных, необходимо определиться с задачами, которые стоят перед маркетинговым отделом. Если бренд не проводит медийные кампании или проводит, но мало, то стоит попробовать модель Маркова из-за ее доступности и простоты внедрения. Но в случае если кампании преимущественно ориентированы на повышение знания о бренде, то есть бюджет распределяется в пользу охватных инструментов, то лучше обратить внимание на более продвинутую и сложную модель по Шепли.